In my last post we looked at the structure of AWS IAM policies and looked at an example of a policy that was too broad. Let's look at a few more examples to explore how broad permissions can lead to security concerns.

Unscoped Service Actions

By far the most common form of broad permissions occurs when policies are scoped to a service but not to specific actions.

Usually, a compute resource needs to interact with the data plane of a service, performing CRUD-like operations to manipulate data inside of a resource made available by the service. An example is a Lambda Function uploading files to an S3 Bucket. Much less frequently do compute resources need to interact with the control plane of a service, which is used to manage resources themselves. Deleting an entire S3 Bucket, for example, is a control plane operation. Most compute resources should only have permissions for specific data plane operations.

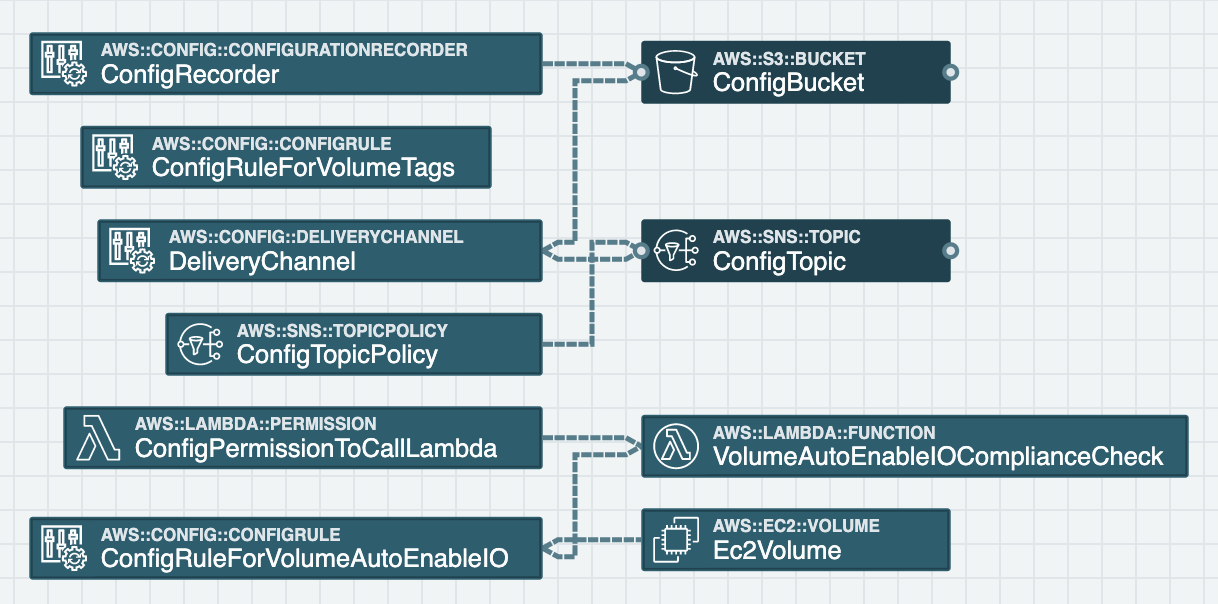
Our first example comes from AWS CloudFormation samples: the "AWS Config delivery channel and rules" template. Let's examine it with stack.new here.

This stack shows how to create an AWS Config Rule to ensure EBS Volumes have a specific Tag and have the Auto Enable I/O functionality turned on. Periodically AWS Config will check whether an EBS Volume is in compliance, write the result to an S3 Bucket, and send a notification of compliance to an SNS Topic.

While the check for tagging is built into the AWS Config service, checking for whether Auto Enable I/O is turned on is not a built-in check. Instead, a Lambda Function is used to check the setting.

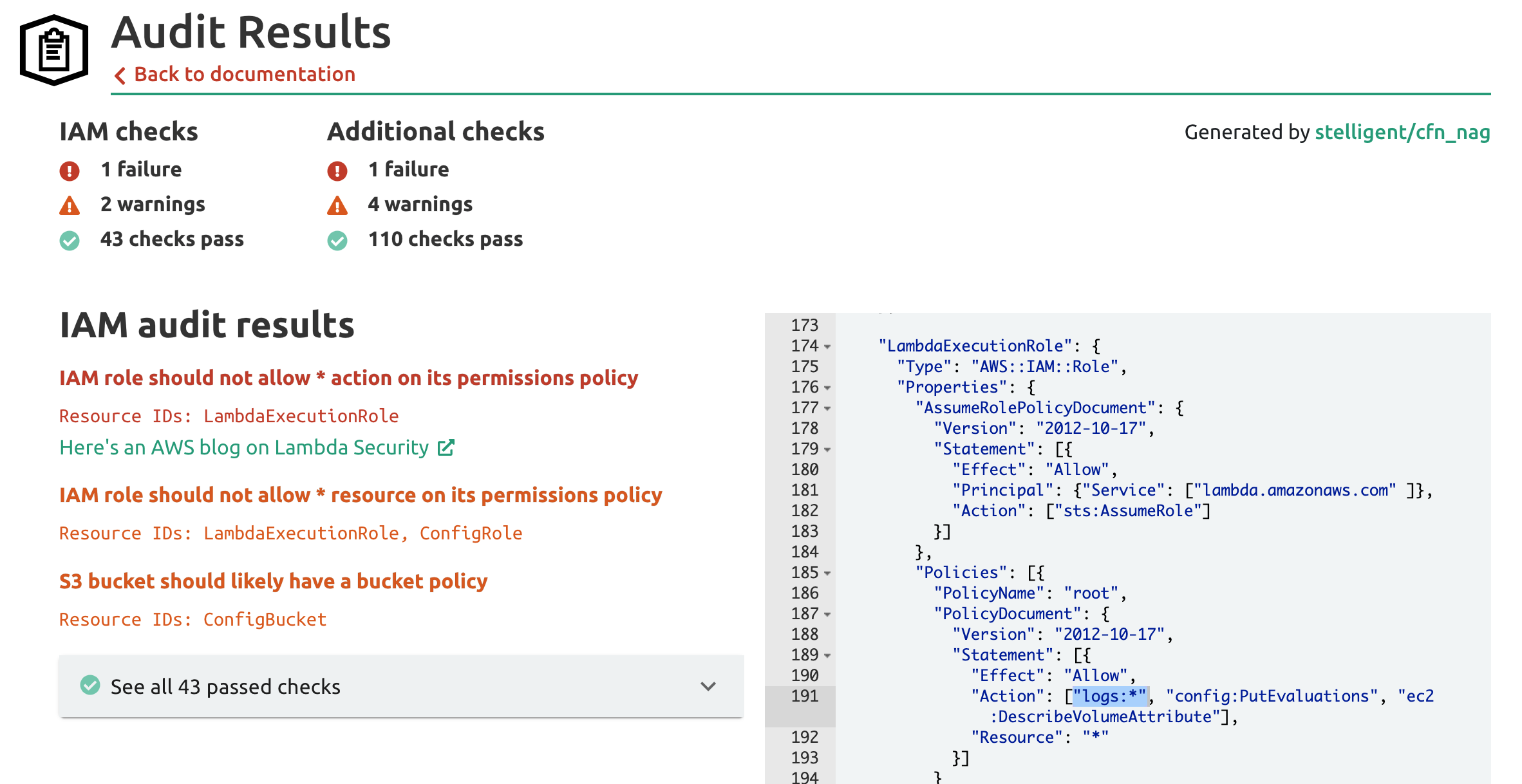
It's in the Lambda Function's Role that we see overly broad permissions. The stack.new audit warns us of the issue:

The Lambda Function is given permission to call any AWS CloudWatch Logs action on any resource. Lambda Functions need permission to send log events to the Logs service, but they don't need unfettered access to the entire control and data plane. With this permission set the Function is also able to create and delete entire Log Groups and Streams. A malicious attacker would find this very helpful in removing information about their exploits!

To remediate this issue we would scope permissions to individual actions and resources. We would want to split this one policy into separate policies for each independent resource type as well: one for the Logs service, one for the Config service, and one for the EBS Volumes service (which has an IAM action prefix of ec2:). We'll see a better solution for scoping Lambda Function Logs permissions in a bit below.

Allow and NotAction Are Not Friends

Sometimes folks try to get tricksy with their IAM policies. While most policies contain only an Effect: Allow statement, a list of actions, and a list of resources, there are other ways one can construct policies. For example, you can create a nicely scoped policy with the following statement:

{ "Effect": "Deny", "NotAction": "s3:GetObject", "NotResource": "arn:aws:s3:::my-bucket/my/file.png" }

Using De Morgan's Law we can state this policy as: Allow the s3:GetObject action on /my/file.png in the my-bucket S3 Bucket, and deny all other requests. While this could be stated using Allow, Action, and Resource properties, stating this as a Deny statements can be helpful in that Deny statements override Allow statements. That makes Deny statements useful in Service Control Policies and Permission Boundaries, where you may want to allow most actions but prevent a few specific ones (like creating static AWS access keys).

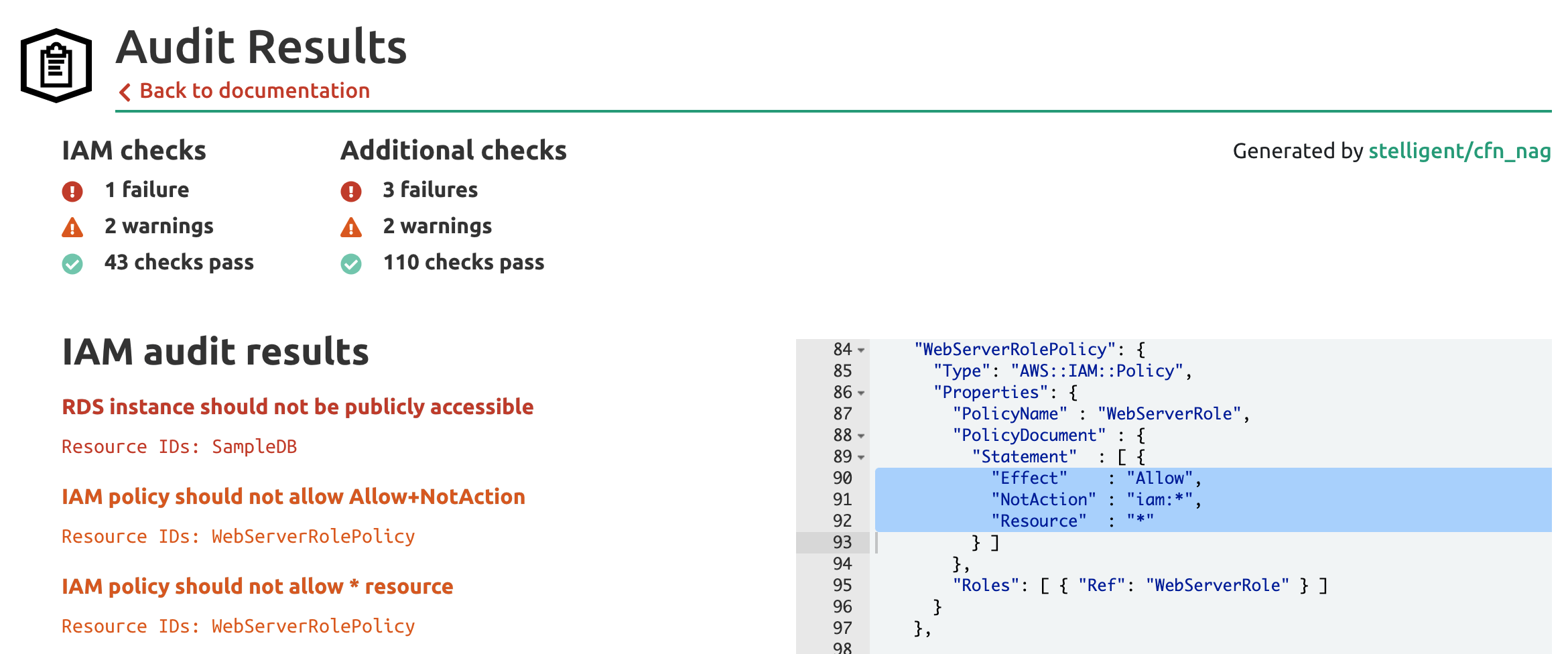
However, sometimes all these properties get mixed up into dangerous combinations. Let's take a look at the AWS CloudFormation sample "Elastic Beanstalk sample application with a database". Let's examine it with stack.new here.

The stack creates an autoscaling application using AWS Elastic Beanstalk and integrates with an Amazon RDS Database for data storage.

The audit results find a handful of serious issues. We're going to ignore the failure for the RDS instance being publicly accessible and focus instead on the IAM policy warnings.

The first warning correctly deduces that we've inappropriately combined Effect: Allow with a NotAction property in our policy statement. What this statement does is allow the EC2 Virtual Machine that Elastic Beanstalk provisions for us to make any AWS action as long as it is not an IAM action. This would allow the machine to create, read, write, or delete S3 buckets, create more virtual machines to mine bitcoins, or potentially connect to and exfiltrate data from databases if they have IAM authentication or the Data API enabled.

This kind of inappropriate policy is believed to be the privilege escalation mechanism used in the Capital One data breach.

The Fix

To remediate this issue, IAM policies should never mix Effect: Allow and NotAction properties in the same statement because it enables unscoped allowances. Even if you were to specify all the services and actions that are not intended to be allowed in the NotAction property (which would be very hard to do), this statement will automatically allow new AWS services and actions released over time.

In this instance, given that the application likely only needs to connect to the RDS database, this WebServerRolePolicy can likely be deleted without any ill effects. Authentication to the database is handled through database-specific credentials, and network connectivity is provided through security groups.

An Example to Live By

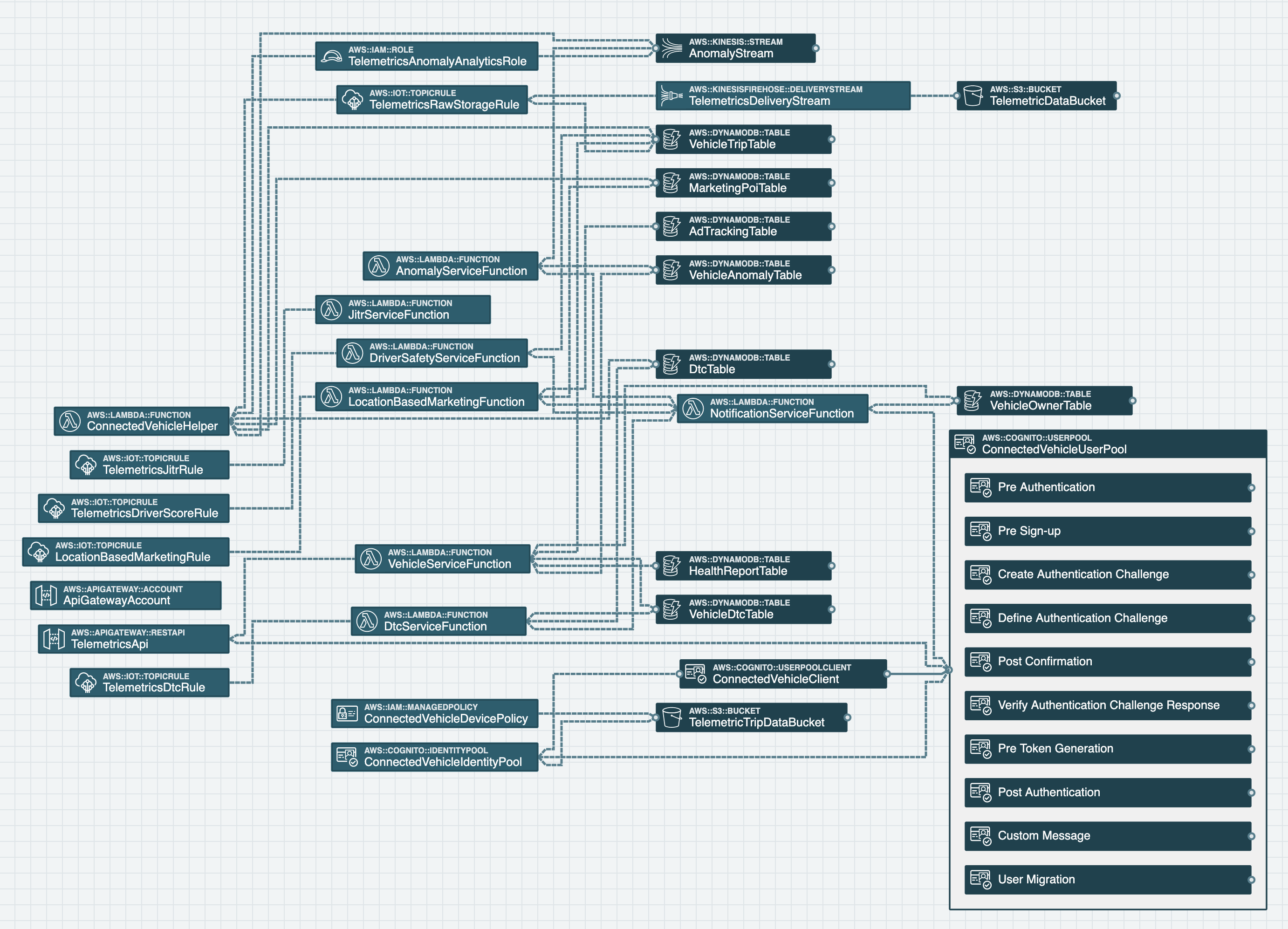
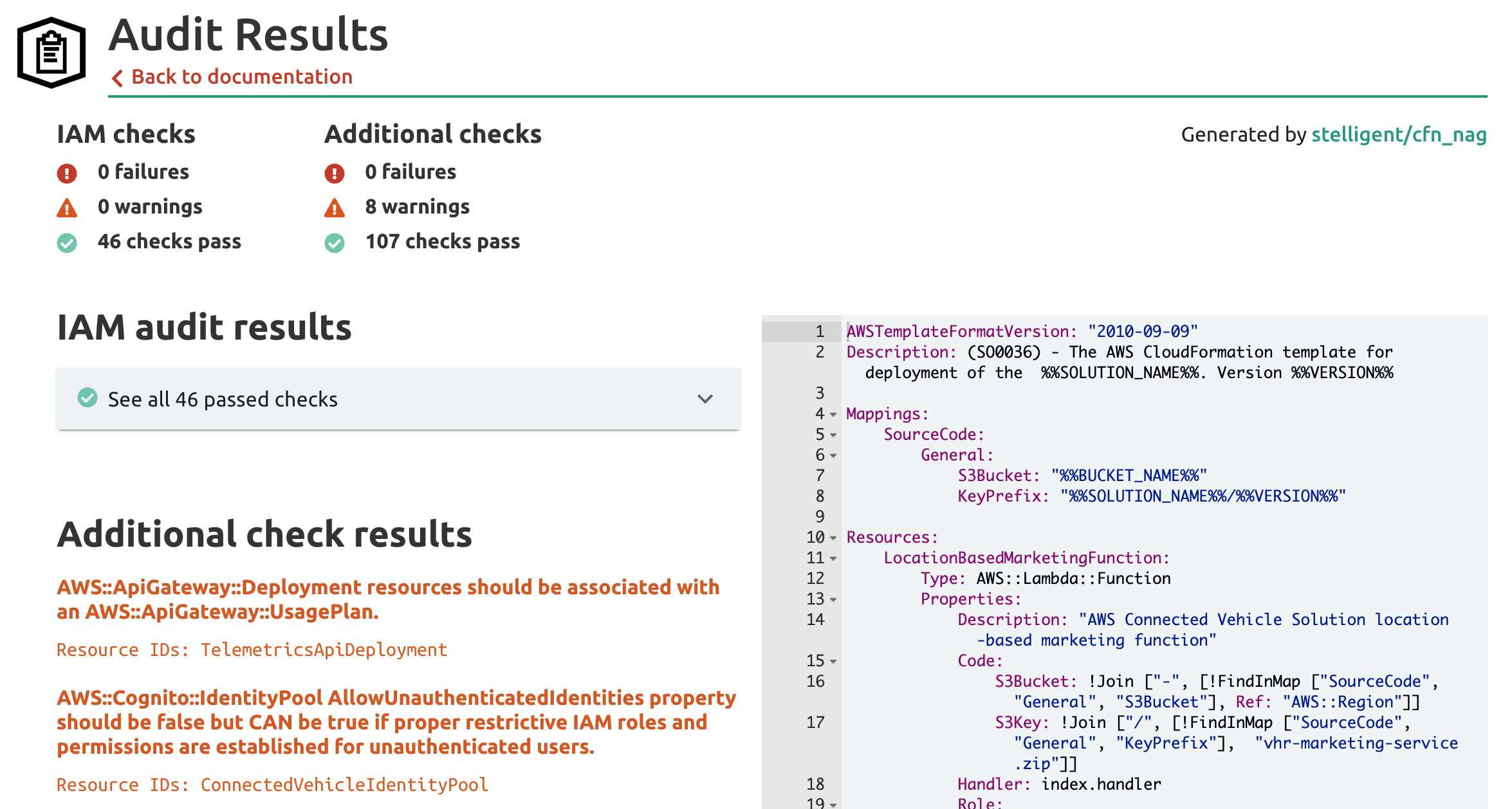
It's hard to write good IAM policies! That's why we should also praise examples that do a great job of showing how to do it well. Let's take a look at the AWS Connected Vehicle Solution. Let's examine it with stack.new here.

AWS Connected Vehicle Solution

The solution shows how one might architect an application to analyze telemetry from vehicle sensors, and is comprised of many different managed services requiring many different AWS IAM policies. Let's take a look at the audit results:

No IAM failures or warnings! Let's take a look at an example policy statement from the AnomalyServiceRole IAM Role that is used by a Lambda Function in the template to see how they accomplish this feat:

- Effect: Allow Action: - logs:CreateLogGroup - logs:CreateLogStream - logs:PutLogEvents Resource: - !Sub arn:aws:logs:${AWS::Region}:${AWS::AccountId}:log-group:/aws/lambda/* - Effect: Allow Action: - dynamodb:BatchGetItem - dynamodb:BatchWriteItem - dynamodb:DeleteItem - dynamodb:GetItem - dynamodb:PutItem - dynamodb:Query - dynamodb:Scan - dynamodb:UpdateItem Resource: - !Sub arn:aws:dynamodb:${AWS::Region}:${AWS::AccountId}:table/${VehicleAnomalyTable} - !Sub arn:aws:dynamodb:${AWS::Region}:${AWS::AccountId}:table/${VehicleAnomalyTable}/index/vin-trip_id-index - Effect: Allow Action: - kinesis:DescribeStream - kinesis:GetRecords - kinesis:GetShardIterator - kinesis:ListStreams Resource: - !Sub arn:aws:kinesis:${AWS::Region}:${AWS::AccountId}:stream/cc-anomaly-stream - Effect: Allow Action: - lambda:InvokeFunction Resource: - !GetAtt NotificationServiceFunction.Arn - Effect: Allow Action: - kms:Decrypt Resource: - !Sub: arn:aws:kms:${AWS::Region}:${AWS::AccountId}:alias/aws/kinesis

We see the following scoping stand out in the policy:

• It has just the right actions to create and write logs in the appropriate namespace for Lambda Functions in AWS CloudWatch Logs.
• It has just the CRUD data-plane actions necessary to interact with the Vehicle Anomaly Table directly and via one specific secondary index.
• It has just the read-only data-plane actions necessary to read records from the cc-anomaly-stream Kinesis Data Stream.
• It has permission to invoke only the Notification Service Function (and no other Lambda actions).
• It has permission to read (in this case, decrypt) data from Kinesis using the built-in AWS KMS key.

Each of these permissions are scoped to just the necessary actions on the necessary resources for the Anomaly Service Function to accomplish its tasks.

Conclusion

Crafting properly scoped IAM permissions is not trivial, but there are many examples to learn from, both good and bad. Thankfully, with tools like stack.new and Stelligent's cfn_nag we can identify the good and bad parts of examples. Give us a shout @stackeryio if you come across great (and not-so-great!) examples you learned from!